本文作者江小白，来自安比技术社区的小伙伴，本系列文章将对 Bulletproof 算法在 Range Proof 和 general arithmetic circuits 上的应用展开介绍。

前言

在本系列的第一篇文章中，我们介绍了Bulletproofs 在 Range proof 上的应用，当 prover 想要证明 v 值在范围[0, 2n-1]内时，他需要发送 2n+7 个元素。然而，这种O(n)级的CC并不是我们想要的，希望能寻找一种方法可以把CC降低到O(log(n)级。本篇我们就主要介绍这个优化过程。主要分为两部分：

1. 以简单的场景去阐述这个优化过程

2. 把第一篇的Range proof结果嵌入到优化过程

注：第一篇文章由于格式的原因，公式显示会有误差，向量的特殊标记也没有显示出来，因此本篇将以图片的形式展示整个过程；另外，本文最后也附上了第一篇文章的图，帮助大家理解^_^

Improved Range proof

01

A simple example

1. 预备知识

aL：表示向量

2n：表示向量

<a,b>：表示向量内积，结果是一个值

a ○ b ：向量对应位相乘，，结果是一个向量

2. 一个简单的场景

Alice 想要证明向量 {a,b} 满足：

Relation：

一个简单的证明过程就是：

prover 把 {a,b}，c, P 发送给 verifier；

verifier 验证 R:成立。

可以看出，交互复杂度是O(n)，接下来目标是将复杂度优化到O(log(n))

3. 复杂度优化到O(log(n))

=> 首先把 c 整合到 P 上，即 R 修改为如下形式：

Relation：

，

此时，交互复杂度为没有变，只是两步验证化成单步验证，为后续的优化做铺垫。

=>定义一个函数映射H，

其中，

注意函数 H 具有加法同态属性，即：

因此，P 可以写成

Proof:

接下来，让我们看一组交互变换的过程：

1.  

   prover 以以下的方式分别计算L，R：

   recall

    

2.  

   prover 发送L，R，P给 verifier

    

3.  

   verifier 发送一个随机数 x 给 prover

    

4.  

   prover 计算,

5. 并且发送 a'，b' 给 verifier

    

6.  

   verifier 利用接收到的计算

7. 校验

Proof

复杂度优化到 O(log(n))

=> 经过上一步骤：Prover 和 verifier 的交互复杂度已经由 2n+4 (P，μ，a，b)降低到了 n+4(P，μ，L，R，a'，b')，离我们的目标 O(log(n)) 还差了那么点意思，该如何做呢？

让我们先回顾上述过程：

优化前：prover 证明有向量 a，b 满足

优化后：证明问题变成 prover 有向量 a'，b' 满足关系（注：此时向量的长度已经减半 n'=n/2）

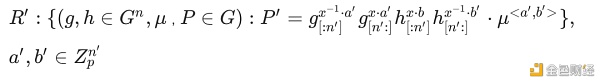
令：

则 R' 转化成：

用 R' 迭代使用上述优化过程，最终 prover 发送给 verifier 的信息如下：

总共 2log(n)+2+2=2log(n)+4 个元素。Oh,yeah!!!

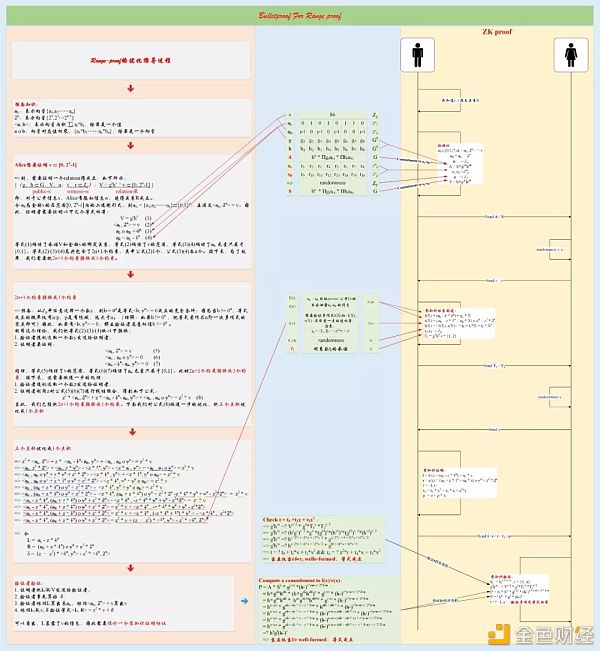
下图是一张基于上述过程的交互协议

有几点需要说明：

1. 图的右半部分分为两个部分

   1. 黄色部分为文章前面部分讲述的过程。这又分为三个部分：

      1. 初始化：省略了P的计算和交互的过程，我们假定开始此证明协议前，验证者已经有了一些基本的信息。这并不严谨，仅仅是为了清晰的表示后面的交互过程

      2. LOOP：一个不断迭代的过程，每次迭代，会:

         1. 产生一对(Li, Ri)，

         2. 所有向量长度减半

         3. Verifier计算Pi' /gi' /hi

      3. End：最后一步，向量 a, b 已减半成常量 a,

   2. 绿色部分为黄色部分的进一步优化，优化思想主要是多次幂乘操作缩减成单词幂乘操作，具体的是：

      1. 上述LOOP中的第3步，延迟到最后一部一次性计算

02

A real Range proof

回顾第一篇文章，我们知道，当我们要证明v属于[0, 2n-1]时，验证者最终要验证：

对关系式做个变换：

因此，prover是要证明有向量 l, r 满足关系：

Relation :

基于此关系，使用上述协议，就可以使 range proof 的交互复杂度降低到对数级。现在，是不是找到点内味了？^_^

总结

本篇文章主要讲到了，BulletProof 是如何把 Range proof 的CC降低到O(log(n))，并且介绍了更近一步的优化。结合第一篇文章，相信你已经对基于 Bulletproofs 的 Range proof 原理有了整体的了解，在本系列的第三篇文章中，将给大家分享 Range proof 的工程上实现细节。

附录

1. Bulletproofs 论文：https://eprint.iacr.org/2017/1066.pdf

2. 附一张图，方便大家理解第一篇文章